難しい知識は不要…小学生でも解けるこの図形問題、あなたは解くことができますか？

食塩水の濃度や往復の平均速度など、仕事などでちょっとした算数の知識が問われる場面に出くわして、ドキッとしたことはないだろうか。「昔は解けたのに……」、そう思うのに解けない。そんな大人たちは本連載で今一度、算数を基礎から学び直してみてはどうだろう。

長年、算数・数学教育に携わってきた桜美林大学名誉教授・芳沢光雄氏の新刊『大人のための算数力講義』(講談社+新書)より抜粋して、「算数の重要な考え方」をお届けする。

『大人のための算数力講義』連載第29回

『円の面積が「半径 × 半径 × 円周率」で求められる理由を論理的に説明できますか？』より続く

前回記事では円の面積が半径×半径×円周率の形で求められる仕組みを述べた。

以下、2つの例題を紹介する(2つ目は少し難しい)。

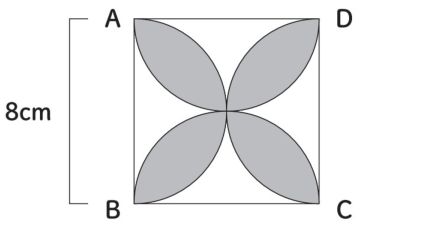
例題:図のように、一辺が8cmの正方形ABCDの中に4つの半円がある。それらの重なる部分の面積を求めよ。なお、円周率は近似値の3.14でなく、を用いるとする。

以下のようにして、求める面積が分かる。

1つの半円の面積=4×4×÷2=8×()

求める部分の面積=4つの半円の面積の合計

-正方形ABCDの面積

=4×8×-8×8

=32×-64()

を得る。

一辺が1の正方形において、各頂点を中心とする半径1の円を4つ描くと、正方形の内側には斜線で示した図形ができる。この図形の面積を求めよ。ただし、一辺が1の正三角形の高さをhとして、hとを使って答えを表すものとする(ちなみに中学数学では、h=(√3)÷2であることを学ぶ)。

問題の図を次のように描き直してみると、以下の式の成立が分かる。

求める斜線でできた部分の面積

=正方形の面積-4×(点々で示した部分の面積)

また、三角形ECDは一辺が1の正三角形なので、

角ECB=角BCD-角ECD=90°-60°=30°

となる。よって、

点Cを中心とする扇形EBCの面積

=1×1××30/360

=÷12=1/12×

が成り立つ。そこで、

点々で示した部分の面積

=点Cを中心とする扇形EBCの面積-弧ECと弦ECに挟まれた部分の面積

=点Cを中心とする扇形EBCの面積

-(点Dを中心とする扇形ECDの面積-正三角形ECDの面積)

=1/12×－(1×1××1/6-1×h×1/2)

=1/12×－1/6×+1/2×h

=1/2×h－1/12×

が導かれたことになる。

以上から、

求める面積

=1×1－4×(1/2×h－1/12×)

=1－2×h+1/3×

を得る。

『全国各地にある「富士見町」から、本当に富士山が見えるかを計算する方法』へ続く