算数が苦手な人にお勧めの「発見的問題解決法」。わからない問題に出会ったら、この「13分類」を考えてみよう

算数嫌いのまま大人になった人たちは「社会に出たら電卓があるから問題ない」「分数なんて実際に使うことはない」「わからなくても生活に困らない」などと言って、算数と無縁の生活を送りがちだ。しかし、あなたの算数嫌いが子ども時代に受けた教育のせいだったとしたら……。

『昔は解けたのに……大人のための算数力講義』（講談社＋α新書）著者の芳沢光雄氏（桜美林大学名誉教授）が、暗記教育で育った人が犯しやすい間違いと、算数を「理解する」ことの楽しさについて解く。

『大人のための算数力講義』連載第32回

『小学生のころはすぐに解けたはず……水と食塩、それぞれ何グラムあれば、10％の食塩水を1000グラムつくれるか？』より続く

「やり方」の暗記とはまったく違う「発見的問題解決法」

昨日の現代ビジネスに載せた拙文「小学生のころはすぐに解けたはず……水と食塩、それぞれ何グラムあれば、10％の食塩水を1000グラムつくれるか？」の最後に述べたように、「割合（％）」の理解では「定義に戻る」（定義や基礎に戻って考える）ことが大切である。

その記事でも述べたが、「く（比べられる量）・も（もとにする量）・わ（割合）」なるものに当てはめて答えを出す「やり方」優先の学びは間違いのもとである。

振り返って筆者は昨年3月に大学教員人生45年が終わり、文系・理系ほぼ半々ずつ合わせて1万5000人の学生を教えた。同時に、90年代半ばから始めた小中高校への出前授業でも、合わせて1万5000人ぐらいの生徒を教えたことになる。その間、「どうやってその証明（解法）を思い付いたのですか」という質問を数多くもらったことが忘れられない。

およそ数学の証明や解答は、一般に筋道が通った洗練された文としてまとめることが普通であるが、それを思い付いた経緯を質問者は聞きたいのであろう。

私はその都度、「いろいろ試行錯誤しながら考えていたら、ふと思い付きました」と、あっさり回答してきた。

しかし、その一方で、心の中では「いろいろ試行錯誤している部分を上手に表現して、学生・生徒の学びの一助とならないものだろうか」と自問したものである。

そこで辿り着いたのが、「発見的問題解決法」の視点を取り入れた学びである。これはパターン化した「やり方」の暗記とは全く異なるもので、解法を導き出す過程での試行錯誤を分類したものである。

この「13パターン」に分けて考えてみよう

人それぞれによって分類法は異なるが、筆者としては下記の13個に分けている。

(1)定義や基礎に戻る

(2)帰納的な発想を用いる

(3)背理法を用いる

(4)条件を使いこなしているか、と自問する

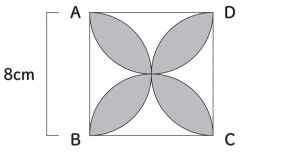
(5)図を描いて考える

(6)逆向きに考える

(7)一般化して考える

(8)特殊化して考える

(9)類推する（構造）

(10)兆候から見通す（経過）

(11)効果的な記号を使う

(12)対称性を利用する

(13)見直しの勧め

本稿では拙著『昔は解けたのに……大人のための算数力講義』（講談社＋α新書）から引用する形で、算数でも上の13個の発想を学ぶことができることを示す。今後の学びや教育の参考にしていただければ幸いである。

数学教育の世界で発見的問題解決法というと、主に高校数学の指導法の一つと捉えられることが普通である。

実際、筆者が東京理科大学理学研究科に勤務していたときのゼミナール生で、発見的問題解決法を研究し、その後は都内の優秀な女子高校の教諭として、指導に用いて成功している者もいる。

一方で、専門数学の本格的な「ガロア理論」の学びでも、実は発見的問題解決法の見方を学ぶことができることを、その方面の拙著を参考にして『数学セミナー』（日本評論社、2023年6月号）で述べたことがある。

「ゆとり教育」で消えた3桁同士の掛け算が、なぜ必要なのか

以下、順に紹介していくが、ごく簡単に紹介させていただく項目もあることをお許し願いたい。

「(1)定義や基礎に戻る」に関しては、定義に戻ることが大切であることを、昨日の「割合（％）」に関する記事で紹介したので、ここでは省略させていただく。

「(2)帰納的な発想を用いる」に関しては、たとえば筆算による3桁同士の掛け算がある。

493×738＝363834

を例にして説明しよう。

筆算による最初の段では、3×8=24の2が十の位に繰り上がり、次に9×8=72にその2を加えて、7が百の位に繰り上がる。このように、次々と繰り上がっていく仕組みを理解するには、2桁同士の掛け算では不十分である。

これはドミノ倒しの理解でも同じで、倒す倒されるだけの2個の牌では不十分で、倒されたものが倒すことにも続く3個の牌が必要である。

実は、この3桁同士の掛け算は「ゆとり教育」で一時、教えなくなってしまった。筆者は2000年当時、その意義を上記のように何度も訴えた。その後、国立教育政策研究所は2006年7月に、「特定の課題に関する調査（算数・数学）」（小4～中3までの約3万7000人を対象）に関して報告をしている。

それによると、小4を対象とした「21×32」の正答率が82.0％であったものの、「12×231」のそれは51.1％に急落。さらに小5を対象とした「3.8×2.4」の正答率が84.0％であったものの、「2.43×5.6」のそれは55.9％に急落したという。

それを機に再び、2桁×3桁や3桁同士の掛け算についても教えるようになってきた。

購入金額とお釣りが、ともに「30円の倍数」のとき、合計は……

「(3)背理法を用いる」に関しては、次の楽しい小話で矛盾を導くところが背理法になっている。

ある日、お母さんは小学生の兄と妹に、「今日は家でパーティがあるのよ。5000円札を渡すから、270円のお弁当を7個と、他に60円のお団子と90円の草もちも適当に混ぜて買ってきてちょうだい」とお遣いを命じた。

お団子屋さんに着くと兄は妹に、

「お釣り、ちょっとごまかして、二人で100円ずつもらって、近くのコンビニで1本100円のアイスキャンディーを1本ずつ買って食べない？　どうせお母さんは算数が苦手だし、忙しいからバレないよ」

と言った。妹も、

「お兄ちゃん、ちょっと悪いことだけど、一緒に仲良くアイスキャンディーを1本ずつ食べたいね」

と返事をした。

結局二人は、270円のお弁当7個と、60円のお団子と90円の草もちをそれぞれ18個ずつ買って、中が見えないように袋に入れてもらった。それらの合計金額は、

　　　270×7＋60×18＋90×18＝4590（円）

となり、二人はお釣りの410円から200円をこっそり取って、コンビニで1本100円のアイスキャンディーを1本ずつ買って食べて帰った。

二人は帰宅するとすぐに、

「お母さん、袋の中にお団子と草もちとお弁当が入っています。ハイ、おつりの210円です」

と言って、お母さんに210円を渡した。

するとお母さんは袋の中を見ることもせず、いきなり、「ちょっと、二人は私にウソを言っているでしょ」と叱った。なぜ、お母さんはそのように叱ることができたのだろうか。

そもそも、お弁当とお団子と草もちの値段はどれも30円の倍数である。そこで、合計代金も30円の倍数になる。そして、お釣りの210円も30円の倍数である。したがって、合計代金とお釣りを合わせた合計金額も30円の倍数にならなければならない。ところが、5000円は30円の倍数ではないので、矛盾である。それゆえ、お母さんは二人のウソを身抜いたのである。

簡単な計算をしてもらって、誕生日を言い当てるクイズ

「(4)条件を使いこなしているか、と自問する」に関しては、25年ぐらいにわたって行ってきた小中高校での出前授業で、必ず喜ばれる「誕生日当てクイズ」がある。

「生まれた日を10倍して、それに生まれた月を加えてください。その結果を2倍したものに生まれた月を加えると、いくつになりますか？」

この質問は、20×日＋3×月の答えを尋ねている。その答えの一つの数を知るだけで、誕生日の月と日がわかるというもので、日は1以上31以下の整数、月は1以上12以下の整数という条件を、巧妙に用いるのである。

本稿では詳しい説明は省略するが、多くの生徒から「えっ、どうしてわかるの？」という質問をいただく。これこそが正に「科学の芽」であろう。

愚直に樹形図を書いてみる

「(5)図を描いて考える」に関しては、昔から「数学の問題は、図を描いて考えるとよい」とよく言われてきた。これをさらに次のように分けて考えたい。

(ア)図を描くことによって、ミスのない思考をする

(イ)実際の図形の検討したい部分を扱いやすい大きさに表現する

(ウ)良いアイデアを生み出すためのヒントを模索する

(エ)各種の統計的なデータを整理して何らかの傾向をつかむ

「(ア)図を描くことによって、ミスのない思考をする」については、樹形図を用いて考えることがある。

たとえば何本も路線図がある地図上で、出発地から致着地に至るルートは何本あるかを求めることがある。ただし、同じ地点は2度通らないものとする。

このようなケースでは、実際に樹形図を描いてすべてのルートをリストアップすると、後で見直しをするときに便利で効果的なものをつくることができる。

樹形図を描くことなく、単に地図の上を何度も鉛筆でなぞる人もいるが、それでは見直しが難しくなってしまうのである。