じつに、美しい…世の数学者を虜にする「平面充填」。なんと、ありうる「回転対称」は、セルによって決まっている、という「驚愕の法則」
天才物理学者・数学者のペンローズが半世紀にわたって探し求めた「アインシュタイン・タイル」の発見について。
ペンローズの幾何学の重要性と人気について。
平面図形に現れる対称性の一例と、回転対称性の限界についての解説。
ノーベル賞学者としても有名な天才物理学者・数学者のロジャー・ペンローズが、1970年代から半世紀にわたって探し求めてきた「ある図形」が話題になっています。
その名は「アインシュタイン・タイル」。
2023年にようやく発見されたその図形とは、いったいどのようなものなのでしょうか?
ペンローズが考案した「ペンローズ・タイル」を超える“幾何学上の大発見”について、ビジュアル重視でやさしく詳しく解説した『ペンローズの幾何学』が刊行され、たちまち大増刷と大きな反響を得ています。
パズル感覚で楽しむことができ、しかも奥深い「平面幾何」の世界を探訪してみましょう。
※この記事は、『ペンローズの幾何学』の内容から再構成・再編集したものです。
前回の記事に続いて、平面図形に現れる対称性について見ていきましょう。まずは「すべり鏡映対称性」から。
「すべり鏡映」とは、一定形状や模様を鏡映にしたうえで平行移動したものを指し、英語では「グライド(glide)」といいます。
前回の記事で登場した「平行移動」と「鏡映」をプラスした移動と考えても結構です。
すべり鏡映の対称性も平面に広がる模様だけがもちうるもので、壁紙のパターンなどでよく使われます。
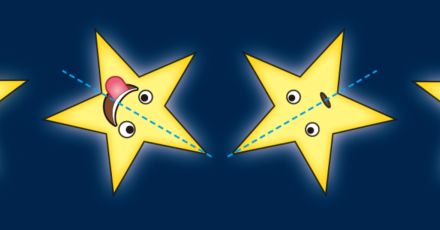
星形や桜の花びらは、中心点で72度(右でも左でも)傾け(回転す)ると、形状がぴったりと重なります。
たとえば右に72度ずつ回転すれば、5回めで元に戻るでしょう。
このような形状は「5回回転対称性がある」、あるいは回転を省いて「5回対称性がある」と表現します。『ペンローズの幾何学』でも、回転という語はなるべく省略しています。
上図の中央に示す「卍」に4回対称性があるのは、説明しなくとも明らかでしょう。
ところが、表面に描かれた内容も含めて考えると、また違うようすが見えてきます。
星形は、縦の線(図中の点線)を軸とする線対称にすぎません。回転すると(1周しないかぎり)元の図形に戻らないからです。
表面の模様を無視して、平面充填模様の場合は、セルだけを考えるなら、ありうる回転対称は180度(2回対称)、120度(3回対称)、90度(4回対称)、60度(6回対称)に限定されます。
72度(5回対称)は、平面充填模様のセルの形状としては無理だというわけです。
また、平面充填模様の場合は、6回対称性より数の多い回転対称も考える必要はありません。たとえば、正十二角形には12回の回転対称性があるでしょうし、円には無限の回転対称性があるのではないかという疑問はそのとおりです。
平面充填模様のセルの形状とは無関係ということにすぎません。